|

Doi:10.1016/j.physa.2004.12.028

Physica A 352 (2005) 113–130 A cell-centered approach to developmental biology Roeland M.H. Merks, James A. Glazier Department of Physics, Biocomplexity Institute, Indiana University, Swain Hall West 159, 727 East 3rd Street, Bloomington, IN 47405-7105, USA Available online 13 January 2005 Explaining embryonic development of multicellular organisms requires insight into complex interactions between genetic regulation and physical, generic mechanisms at multiple scales.
As more physicists move into developmental biology, we need to be aware of the ‘‘cultural''differences between the two fields, whose concepts of ‘‘explanations'' and ‘‘models''traditionally differ: biologists aiming to identify genetic pathways and expression patterns,physicists tending to look for generic underlying principles.
Here we discuss how we can combine such biological and physical approaches into a cell- centered approach to developmental biology.Genetic information can only indirectlyinfluence the morphology and physiology of multicellular organisms.DNA translates intoproteins and regulatory RNA sequences, which steer the biophysical properties of cells, theirresponse to signals from neighboring cells, and the production and properties of extracellularmatrix (ECM).We argue that in many aspects of biological development, cells' inner workingsare irrelevant: what matter are the cell's biophysical properties, the signals it emits and itsresponses to extracellular signals.Thus we can separate questions about genetic regulationfrom questions about development.First, we ask what effects a gene network has on cellphenomenology, and how it operates.We then ask through which mechanisms such single-cellphenomenology directs multicellular morphogenesis and physiology.This approach treats thecell as the fundamental module of development.
We discuss how this cell-centered approach—which requires significant input from computational biophysics—can assist and supplement experimental research in developmental Corresponding author.Tel.: +1 812 855 3735; fax: +1 812 855 5533.
E-mail addresses: [email protected] (R.M.H. Merks), [email protected] (J.A. Glazier).
URL: http://biocomplexity.indiana.edu.
0378-4371/$ - see front matter r 2005 Elsevier B.V. All rights reserved.
doi:10.1016/j.physa.2004.12.028 R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 biology.We review cell-centered approaches, focusing in particular on the Cellular PottsModel (CPM), and present the Tissue Simulation Toolkit which implements the CPM.
r 2005 Elsevier B.V. All rights reserved.
PACS: 87.18.Bb; 87.18.Hf; 87.18.La; 89.75.Fb; 89.75.Kd Keywords: Computational biology; Cellular Potts Model; Cell-oriented modeling; Biological ontologies; Developmental biology As physicists attempt to apply physical approaches to elucidating biological problems (biological physics as opposed to biophysics), they need to be sensitive tothe fundamental differences between biological and physical epistemology, whichreflect the different histories of the two fields particular, the apparentlyinnocuous term model can cause instant misunderstanding.In biology, anexperimental model is a standard organism, e.g. a rat or a fruit fly, which exhibitsa particular biological phenomenon of interest.A theoretical model, or simply amodel is a conceptual model, which describes a hypothetical mechanism using textand qualitative diagrams of interactions.Such a model is successful if it is compatiblewith qualitative observations and suggests further experiments that could support orreject its hypotheses.We will refer to such models as biological models or conceptualmodels.
Biological models, from those describing the structure and function of DNA to the elaborate diagrams describing metabolic and regulatory pathways or the patterningof tissues during development, have had tremendous success and have led to thecurrent era of genomics and proteomics.However, the success of genomics hascaused difficulties, which expose the limitations of classical biological models.Thesuccess of genomics and the need to simplify sufficiently to develop conceptualmodels leads to typical statements of the form ‘‘Gene X causes cancer,'' to which aphysicist would object that a gene, which is simply an embodiment of information,cannot cause anything directly.High-throughput experimental procedures, includingDNA sequencing, microarray analyses, and high-throughput mutation studies, haveshown that the number of interacting players in biological processes is so large that‘‘mentally juggling'' them in conceptual models has become impractical, especiallysince behaviors usually arise from complex networks of interactions rather than fromthe behaviors of individual components.Parallel developments in the physics ofcomplex systems have shown that ensembles consisting of large numbers ofinteracting components exhibit collective behaviors that we cannot always under-stand intuitively from the behaviors of the individual components.We call such anapproach systems biology (see in contrast to a reductionist, geneticessentialist approach.
Epistemologically, biologists have considered explanations to be satisfactory when they can list the elements of a biological process and their connections.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Integration of experimental results
through computational systems biology
Identification of key molecular and cellular players Measurement of cellular phenomenology Integration into computational model Validation of patterns and statistical observables Disconnected experimental facts
High-throughput parameter searches of mechanisms of development
Suggestion of further experimental work Fig.1. Schematic description of the systems biology approach.
Metaphorically, the biological model of a car would list all of its parts and theirinterconnections.A systems-biology approach would include thermodynamics,mechanics, and relevant aspects of chemistry and physics to describe the interactionsand functioning of those elements.At the simplest level, the difference in focus iswhether we frame questions to answer ‘‘what'' or ‘‘how.'' Thus, paradoxically, additional information has made the most central biological tool for generating new knowledge and understanding—the conceptual model—muchless helpful.To correctly integrate this wealth of information and to use it togenerate new hypotheses, systems biology extends traditional conceptual models intomathematical models.Because such models are generally too complex for analyticsolution, we translate them into sets of algorithms or computational models, which wethen implement as simulations.
These problems are particularly evident when we focus our attention on developmental biology, where a genetic essentialism called positional information,which the intellectual school founded by Lewis Wolpert has pioneered andchampioned, has come to dominate .However useful, the concept of positionalinformation has led to an unfortunate focus on genetic experiment at the expense ofother types of measurement.At the same time, even a simple, back-of-the-envelopecalculation reveals that development based on the highly specific genetic signaling ofpositional coding would require much more information than that present in thegenome and that the mechanism is not robust to perturbations.Instead, as Turingobserved in 1952 development must self-organize under the control of geneticregulation.Cells do not merely sit at a given location and respond passively toexternal signals, they move, often over long distances, and actively create the signalsto which they respond.Thus, the concept of a prepattern in which cells migratetowards or respond to a pattern formed by an independent, initiating mechanism hasonly limited utility.Salazar–Ciudad et recently called such prepattern-dependent mechanisms morphostatic, as opposed to morphodynamic mechanisms inwhich cell-signaling, migration and growth occur simultaneously, and arguedthat morphodynamic mechanisms have evolutionary significance because theyenable more phenotypic variation for less genotypic variation.Thus, to under-stand the dynamics of development, and its evolution, we need to return to cell R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 biology and physiology, which have become somewhat unfashionable in thecurrent genomics rush and in which the experimental technology, while benefitinggreatly from advances in gene control, microscopy, microsurgery, labeling andmany others areas, has made much less progress than the technology for puregenomics and proteomics.
2. Modeling issues Computational approaches face their own difficulties, many of which arise from the range of length scales of biological structures and behaviors.Biologicalphenomena range from those which require quantum-mechanical treatment at theatomic level ð1010 mÞ; e.g., the effect of photons on chlorophyll or rhodopsin,through the semi-classical treatment of molecular dynamics ð109 mÞ and theclassical treatment of macromolecules ð108 mÞ; up to agent-based models ofpopulations 103 mÞ: Multi-scale modeling has not yet had overwhelming success in other disciplines (e.g., weather prediction, materials science and geophysics), and where it has, themethods developed for particular problems have tended not to generalize.Thecurrent focus of funding agencies (e.g., the National Science Foundation/NationalInstitutes of Health joint Initiative on Multiscale Modeling) and journals (e.g., thenew Society for Industrial and Applied Mathematics Journal on Multiscale Modelingand Simulation) on the development of multi-scale technique illustrates its intrinsicimportance and difficulty.
Physicists are trained to believe that even very complex phenomena result from the interactions of very few, very simple underlying rules, where the complexity oftenresults from the initial or boundary conditions.A biologist's caricature of aphysicist's approach would be to say that the physicist asserts that ‘‘development issimply a problem in pattern formation,'' writes down a set of differential equationsand a model of the fertilized egg and tries to deduce a chicken.
Besides the inherent arrogance and doubtful success of such an approach, biology generally lacks the homogeneity which makes physical problems tractable and whichpermits powerful calculational simplifications like renormalization-group analysis.
In addition, evolutionary contingencies mean that universal rules of the type whichgives physics its predictive power, need not exist in biology.We cannot assume thatsimplified models will have the same qualitative behaviors as a more complicatedreality, or that observations made in one context will apply to another, even in anapparently similar situation (hence, the widespread feeling among biologists thatphysical models are ‘‘irrelevant'').Thus model validation becomes even moreimportant in biology than in physics and hard-won results may have much morelimited ranges of application.On the other hand, we do observe regularities inbiology, which give hope that we can indeed generalize, e.g., that most individualcells in a frog are indistinguishable from analogous cells in a human, that certainenzymes and regulatory pathways are identical in yeast and mammals or that cells inall multicellular organisms communicate via secreted products and adhesion.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 One specific difficulty is that a simulation can only ever prove sufficiency.It can never prove that a mechanism is correct, nor that a model has included all significantcomponents.Physicists, who believe in Occam's razor, can never directly rebut thecomplaint ‘‘But you have left out . .'' Only when simulations can prove their utilityby predicting (rather than ‘‘post-dicting'') experimental observations, will biologistsbe willing to accept this difference in philosophy.
Thus, biological problems are intrinsically specific, heterogeneous and multi-scale.
A computational treatment of a particular problem must begin by choosing anappropriate scale or level of detail, which the inclusion of additional scales can laterrefine.What is the appropriate first level at which to address development? Many computational-biology studies of development focus on tissue-level phenomena, modeling tissues as continuous elastic solids or visco-elastic fluids.
Others aim to generalize from an understanding of single-cell behaviors anddynamics, building microscopic models of intracellular dynamics (e.g., electro-physiological models or single-cell models of filopodial extension).Some authors(e.g., ) argue that coupling many detailed single-cell models can produce models ofmulticellular phenomena.Molecular and subcellular models like Virtual Cell Silicon Cell1 or E-cell provide great detail on aspects of subcellular processes.
These projects ultimately aim to produce a detailed cell-replica.However worthwhilethis aim, such replicas would be just as complex as the biological cells they modeland be just as hard to understand.In addition, they can, at best, treat small clustersof a few to tens of cells.
Even if subcellular models replicated aspects of multicellular behavior, could we then say that we understood the behavior? As physicists, we feel that in order tounderstand a natural phenomenon, we must generate simplifying abstractionsorganized around common principles of behavior at the appropriate level.Goingback to our car metaphor, constructing a functional car replica with LEGO brickssimply by copying one-by-one all the steps in an instruction book does notnecessarily teach us how a car functions.We obtain insight and understanding byidentifying general functional modules like engines, gear-trains, and differentials,observing how they function, how these functional modules interact anddistinguishing their universal underlying rules from accidental details such as paintcolor, choice of metal, or six vs.eight cylinders.Working at too coarse or fine a levelof detail makes such an analysis much harder.
The cell provides a natural level of abstraction for mathematical and computa- tional modeling of development.Treating cells phenomenologically immediatelyreduces the interactions of roughly 1052106 gene products to 10 or so behaviors:cells can move, divide, die, differentiate, change shape, exert forces, secrete andabsorb chemicals and electrical charges, and change their distribution of surfaceproperties.
Is ignoring (to a first approximation) intracellular behaviors legitimate? In a recent book review Meinhardt stated that ‘‘The role of the cell as a moduleof development can hardly be overestimated.'' Indeed, much of the biology of R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 multi-cellular development treats the individual cell's internal properties as a ‘‘blackbox:'' for example, the function of an inductive signal does not depend on whathappens ‘‘behind the scenes,'' (e.g., on the number of elements in a signal-transduction cascade) as long as the cells respond correctly to the signal.Recentlyvon Dassow and Meir drew a parallel between object-oriented computerprogramming and modularity in biology.Object-oriented programs consist ofmodules, the objects.These objects have well-defined interfaces, through which weaddress all functionality of the object.In object-oriented programs, data hiding isessential: as long as we do not alter the object's response to requests from otherobjects, we are free to change the object's inner workings.von Dassow and Meirargued that ‘‘nature cannot do data hiding'' although they conceded that ‘‘theclosest thing to data hiding ½. . is cellular compartmentalization.'' We argue thatnature's solution to data hiding is the cell, where signaling molecules (either on thecell surface, or secreted, diffusive signals) and receptors implement the objectinterface.If nature itself uses individual cells as an abstraction, why should we makeour biological models more complicated by describing tissue-level structures in termsof subcellular behaviors, which do not affect it directly? Could we ignore cells and model at the level of tissues? Ignoring cells is dangerous.
Macroscopic models, which treat tissues as continuous substances with bulkmechanical properties (e.g., Physiome ) reproduce many biological phenomenabut fail when structure develops or functions at the cell scale.Although continuummodels are computationally efficient for describing non-cellular materials like bone,extracellular matrix (ECM), fluids and diffusing chemicals, many cell-centeredmodels reproduce experimental observations missing from continuum models.
We feel that cell-centered models are essential tools in developmental biology.
Cell-centered models use phenomenological models of individual cells to study howthe collective behavior of multiple simplified cells drives tissue-level and organism-level processes.The relative simplicity of cell-centered models allows simulation of1052106 cells on a single processor, ultimately making whole-organism simulationspractical on parallel computers. shows the hierarchy of scales we include inour models.The questions we can answer with a cell-centered model include: Howdoes the genetic program interact with generic mechanisms to form an organ? Whatare the relative contributions of local and long-range signaling? What specific factorsresult in abnormal growth? Building a cell-centered model requires several steps.First, we infer individual cell behaviors from biological experiments.We can often obtain cell-behavior data fromthe scientific literature, including the cell's morphology, its response to extracellularand contact-dependent signals, its adhesion to other cell types and the ECM, itschemotactic and haptotactic motility (cell movement in response either to chemical,mechanical or textural gradients in the ECM), the cells into which it can differentiateand the signals which induce differentiation.We may also need to performadditional experiments to obtain precise, quantitative data on cell behavior.Once wehave identified how individual cells behave, we can describe the essentials in aconceptual biological model, which we then translate into a mathematical model andimplement computationally.This computational description phenomenologically R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Fig.2. Cell-centered modeling methodology.
reproduces the individual cells' behaviors.The phenomenological single-cell model ispurely descriptive and has no explanatory value per se.It becomes useful when wesimulate many single-cell models simultaneously to determine whether the behaviorswe included in the single-cell model suffice to explain the tissue-level patterns andphysiological functions we find in experiments.If the simulation does not matchexperimental observations, we return to the experiment to investigate which elementsare missing, or which parameter values are inaccurate.High-throughput parameterstudies can map out the alternative behaviors of the model, to determine if otherparameter combinations better match the experiments.If so, we must either repeatthe experimental measurements of sensitive parameters, or determine whether wehave missed an essential element of single-cell behavior that a specific parameterchoice can mimic.If the model results match experimental observations, we canfurther test our model by making experimental predictions.What happens to the cellensemble if we eliminate one of the single-cell behaviors? Can we remove the sameelement in an experiment, e.g., with a genetic knock-out, and find similar tissue-levelensemble behavior? Thus, by introducing cell-centered simulation into the empiricalcycle we can identify the minimal set of single-cell behaviors which suffices toproduce certain tissue-level behaviors.We can then ask which networks of genes steerthis set of single-cell behaviors and how they do it.In this way, we can preciselydescribe and understand the role of gene networks in multicellular phenomena, R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 instead of merely observing that knocking out a gene disrupts a multicellularfunction.
Several cell-centered computational approaches exist to study morphogenesis in cell aggregates and tissues.These models aim to reconstruct tissue dynamics from thecollective behavior of the individual cells.Although some of these approaches keepthe position of the cells relative to each other fixed (such as in plant tissues) (see e.g.,Refs. most focus on animal tissues, which consist of mobile cells.Suchmodels simulate aggregates of hundreds to tens of thousands of cells, and accountfor the adhesive forces between cells and between cells and ECM, as well aschemotactic and haptotactic movements.Palsson et carry out Newtonianforce calculations between individual ellipsoidal cells, to recover the viscoelasticbehavior of cell-aggregates and simulate differential-adhesion-driven engulfment ofone cell type by another.Another approach is to model aggregations of cells oranimals using cellular automata or lattice gases ).In lattice gases,individual particles that live on a discrete grid represent cells, hopping from onelattice node to the next depending on their discrete velocities.This approach formodeling morphogenesis applies, e.g., to studies of ripple formation in myxomycetes, germinal center dynamics and avascular tumor formation do et al.
introduced a Lagrangian Monte-Carlo method, where attraction, compressionand bending energies determine movements of spheroidal cells.Drasdo et al.haveused their method to simulate cleavage and gastrulation and avascular tumorgrowth ly, Newman and Grima developed a statistical-mechanicsapproach to modeling chemotactic cell–cell interactions.Their Langevin-dynamicsapproach allowed them to study cell ensembles analytically.In the mean-field limittheir method recovers the Keller–Segel equations for chemotaxis and co-workers used the Netlogo2 agent-based modeling environment to model cell–cellinteractions.In this environment, individual agents move on a square latticeaccording to a set of preprogrammed rules and the local environment of the agents.
Netlogo cannot directly account for cell adhesion, which Peirce et al.explicitlyprogrammed into the agent rules.Peirce et al.applied Netlogo to simulatemicrovascular remodeling and blastocoel roof thinning during gastrulation ofXenopus laevis The Cellular Potts Method (CPM) is a convenient and powerful mesoscopic method for modeling cell membrane, cell and tissue dynamics, retaining individualcell identity.Glazier and Graner developed the CPM to simulate differential-adhesion-driven cell rearrangement resulting from cell adhesion molecules (CAMs),and quantitatively reproduced cell-sorting experiments.
Additions and improvements to the CPM algorithm include cell growth, cell division, apoptosis and cell differentiation chemotaxis extracellularmaterials and cell polarity Hogeweg, pers.comm.).The CPM is becominga widely used computational tool in the study of biological morphogenesis, rangingfrom the full development of the cellular slime mould Dictyostelium discoideum, to skeletal formation in the vertebrate limb R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 The remainder of this paper briefly introduces the CPM and illustrates its applications in developmental biology.We conclude with a comparison of the CPMto alternative cell-centered methods.
3. Cellular Potts model The fundamental choice of the CPM is to represent most cell behaviors in the form of terms within a generalized energy H, which includes the interactions between cellsand other cells and the ECM and constraints which determine individual cellbehaviors.The genetic regulation of the cell then determines the parameters in theseenergy terms.We can solve the dynamics of such an energy formalism using a varietyof methods, including finite-element, diffuse-boundary, sharp-interface and others.
The ordinary CPM we describe below uses a lattice-based Monte-Carlo method withMetropolis dynamics and a generalized Boltzmann weighting function because theseare the simplest choices/assumptions.However, we could use off-lattice methods,deterministic dynamics, Kawasaki dynamics and non-Boltzmann weighting func-tions if they were more computationally efficient or if they better reflected newbiological data.
The CPM represents biological cells as patches of lattice sites, x; with identical xÞ; where each index identifies, or ‘‘labels'' a single biological cell.
Connections between neighboring lattice sites of unlike index sð membrane bonds, with a characteristic bond energy Jtðs xÞ;tðs x0Þ; where the cell types t(i.e., endothelial, epidermal, etc.) determine the adhesion strength of the interactingcells.An energy penalty increasing with the cell's deviation from a designated targetvolume As imposes a volume constraint on the biological cells.A similar energypenalty on deviations in cell surface area from a target area Ss constrains the amountof cell membrane.To mimic cytoskeletally driven membrane fluctuations, werandomly choose a lattice site, x; and attempt to copy its index s x into a randomly chosen neighboring lattice site x0: We reduce the effects of lattice anisotropy by using the 20, first- to fourth-order neighbors on a square lattice.On average, we attempt anupdate at each lattice site once per Monte-Carlo step (MCS).We calculate howmuch the energy would change if we performed the copy, and accept the attemptwith probability: PðDHÞ ¼ fexpððDH þ H0Þ=TÞ; DHX  H0; 1; DHo  H0g , where H040 is an energy threshold which models viscous dissipation and energyloss during bond breakage and formation .We then define the Hamiltonian as: where l represents resistance to compression, l0 resistance to membrane stretching,as is the current cell volume, ss the current cell surface area and the Kronecker deltais dx;y ¼ f1; x ¼ y; 0; xayg: The cells reside in a ‘‘medium'' which is a generalizedCPM cell without a volume constraint and with s ¼ 0; t ¼ 0: We can define the

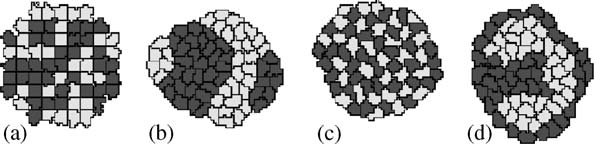
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Fig.3. Simple setup of the Cellular Potts Model (CPM) Initial condition.Using different bond-strength settings between dark cells (d), light cells (l) and the surrounding extracellular matrix (E), weobtain (b) cell sorting (gld 40; glE ¼ gdE40), (c) mosaic cell ordering (0ogld; glE40; gdE40), and (d)engulfment, with the position of high and low adhesivity cells inverted (g surface tensions gt Þ=2; which enable us to determine whether energetics favors homotypic ðg 40Þ or heterotypic bonds ðg (see usually define a special high cell-border energy to prevent cells fromadhering artificially to the lattice boundaries.The viscous dissipation H0 and allterms in the energy, i.e., the bond energies J, and the prefactors to the additionalenergy terms, such as l; scale with the temperature T; i.e., if we multiply T by a factort; we can multiply H0 and the energy by the same factor and obtain the samesimulation results.
Savill and Hogeweg introduced an elegant method to model chemotaxis in the CPM.They used a discretized field C for the concentration of a chemoattractantchemical, defined a set of ordinary differential equations (ODEs) within each cellthat describe the cell's secretion and absorption of the chemical, and a set of partialdifferential equations (PDEs) to calculate the diffusion and decay of the chemical,ignoring advection.They then caused cells to preferentially move up chemoat-tractant gradients, by adding a term to the energy: where the original method sets s, a Michaelis–Menten constant, to 0.Other authorshave used a similar method to model haptotaxis.
Hogeweg introduced cell differentiation, cell division and apoptosis to the CPM in a study of the evolution of multicellular development.She used the state of aBoolean network —a simple model of the genetic regulatory network—withinputs from neighboring cells, combined with a simple lock-and-key model of CAMsto determine the bond-energies J.With similar methodologies we are currentlyintroducing more realistic models of genetic regulation into the CPM.Alternativemethods for cell differentiation simply use preprogrammed type ðtÞ changes of thecells weg modeled cell division by assigning a new s to the grid points onone side of the shortest axis of the cell.To implement cell death, she simply set thecell's target volume A to zero, after which the cell vanishes in a few MCSs.Hogewegimplemented cell growth by slowly incrementing the target volume; by consistentlydoing so when the cell's actual surface area exceeds its target surface area, the celldevelops a turgor pressure, which can account for meristimatic growth.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Zajac et al. developed a method to account for anisotropic differential adhesion, through the polar distribution of cell-adhesion molecules.They used ashape constraint favoring elongated cells.The bond energy J is highest (weakestadhesion) between two cells touching at their apical and basal surfaces, while itdecreases (stronger adhesion) for cells adhering laterally.Zajac's method was slowðOðN2ÞÞ: However, we have developed an efficient ðOðNÞÞ calculation of the neededcenters of mass and moments of inertia of the cells which runs after each update ofthe cell boundaries Most groups using the CPM methodology either developed their own code or hard-coded modifications of previous code.Now, several groups are collaborating todevelop an open-source CPM simulation environment that contains the basicfunctionality CPM models need, and allows easy and transparent extension.Suchsimulation environments should reduce the overhead in setting up new CPM-basedsimulations.Just as we do not want to develop from scratch or even tweak the sourcecode of our word processor every time we write a paper, we do not want to redefinethe CPM every time we want to set up a cell-oriented simulation.A commonenvironment also allows sharing and archiving of new modules to describeadditional biological mechanisms (e.g., an anisotropic adhesion module or detailedmodels of intracellular genetic regulation).The environment model also allowsunified approaches to coupling the CPM with microscopic models like BioSpice3 andmacroscopic models like Physiome.The main current CPM simulation environmentis CompuCell3D 4 With CompuCell3D researchers can set up a simulation usingthe scripting language XML.The environment's architecture is very flexible.Userscan add new energy functions, additional constraints, initial conditions andvisualization methods by writing plug-ins in C++, analogous to the plug-ins mostmodern web browsers use.We are currently working to develop a morecomprehensive environment, the Tissue Simulation Toolkit,5 combining Compu-Cell3D with a C++ library for the two-dimensional CPM which we have written incollaboration with Paulien Hogeweg at Utrecht University, The Netherlands.Ouraim is to develop a cell-centered simulation environment, which becomes a part ofthe developmental biologist's workbench, just as bioinformatics and image analysistools have.
4. The CPM in developmental biology The collage in illustrates the wide range of problems life scientists have addressed with the CPM.Hogeweg used the CPM to study how evolvinggenetic regulatory networks interact with generic mechanisms, such as cell sorting,engulfment and intercalation to produce a complicated body plan duringdevelopment (-mir and De Boer explained all-or-nothing clonal

R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Fig.4. Cellular Potts modeling in developmental biology.(a) Evolution of developmental mechanisms, weshow gastrulation-like mechanism here (b) clonal selection of b-cells in the germinal center throughcompetition for contact with the (large) antigen-presenting cell (c) tumor invasion (d) Notch-Delta mediated stem-cell cluster-size control in the human interfollicular epidermis ; (e) mesenchymalcondensation through cell–ECM interactions (f) convergent extension ; (g) endothelial cells,secreting VEGF-A, chemotactically aggregate to form a vascular network ; (h) limb bud outgrowth, achemotactic signal from the apical ectodermal ridge (shown in black) causes the asymmetry (Zeng,Thomas and Glazier, unpublished); (i) formation of a fruiting body in Dictyostelium discoideum selection of b-cells during affinity maturation in the germinal center as a competitionfor adhesive contact to antigen-presenting cells, which they elegantly modeled usingthe CPM (b).The CPM, like other cell-centered techniques, can provide insightinto tumor progression.With the CPM we can straightforwardly evaluate the rolesof cell–cell and cell–ECM adhesion in malignant tumor invasion, as Turner andSherrat and Turner et al. have demonstrated c).
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 The CPM is especially useful to study patterning in tissues.Savill and Sherratt combined a subcellular ODE model of membrane-bound Delta-Notch signaling witha discrete-state differentiation model to compare the ability of several hypotheticalscenarios to explain clustering of stem cells in the human epidermis (etal. suggested a non-Turing mechanism to explain clustering of mesenchymal cellsduring cartilage patterning, where cell-secreted fibronectin enhances adhesionbetween mesenchymal cells and the ECM (a previous continuummodel Merks et al. developed a cell-centered, chemotaxis-driven model ofvasculogenesis (of the feedback between cell movement, celladhesion and secretion/diffusion, these cell-level models exhibit qualitative behaviorsmissing from their continuum PDE limits—an important example of the need forcaution in interpreting PDE results.
f, h and i illustrate how we can use the CPM to obtain insight into tissue- level mechanisms of morphogenesis.Zajac et al.modeled convergent extension,a developmental mechanism which, shortly after gastrulation, elongates certainvertebrate embryos (showed that anisotropic intercellular adhesionand cell alignment suffice to produce many aspects of convergent extension.Zeng,Thomas and Glazier (unpublished) showed that chemotaxis toward the apicalectodermal ridge suffices to produce the asymmetric shape of the growing chick limbbud (a beautiful hybrid CPM–PDE model of D. discoideummorphogenesis, Mare´e and Hogeweg showed that a peristaltic mechanism canexplain the formation of the stalk of the fruiting body of D. discoideum (Pressure waves—caused by the amoebas' chemotactic movement towards excitatorycAMP waves—drive the stalk downwards.
All these studies employed phenomenological models of individual cell behaviors and communication to reproduce and explain experimentally- observed tissue-levelbehaviors.How can we validate such cell-centered models? First, we mustquantitatively compare the simulations with experiments.The CPM provides awide range of measurements, which we can directly compare with experimentalmeasurements, including tissue patterns, cell positions and velocities, pressure causedby migration or shape changes of cells, cell morphology, surface tensions andmorphogen concentrations.We are not yet able, however, to obtain informationabout the action and reaction forces the cells exert on the medium.We cannot expectcells to take precisely the same migratory paths in simulation and experiment, sincethey follow different paths in repeated experiments.Instead, we must compare thestatistics of cell-migration to the final pattern.
We must be cautious, however, because different biological mechanisms can produce similar patterns.For example, continuum models assuming chemotaxis-driven cell migration and strain-driven cell migration both reproduce aspectsof in vitro vascular patterning.We may be able to distinguish between suchalternative patterning mechanisms by tracking patterning over time.For example, ina chemotaxis-driven model we expect cells to speed up as they approach each otherbecause the interplay between chemoattractant secretion, diffusion and decay createsexponential chemoattractant gradients around the cells.In a strain-driven model wewould instead expect linear dynamics.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 Genetic knock-outs are powerful tools for verifying the hypotheses underlying cell-centered models.We can introduce the genetic knock-out's phenomenologicaleffects on individual cell behavior into our cell phenomenology and study how themodified cell behavior alters tissue patterns and mechanisms.We are currentlyapplying such an approach to validate our vasculogenesis model (onlydoes reproducing the tissue-level effects of knock-outs help validate our computa-tional models, it also helps us unravel the role of particular genetic regulatorynetworks.Only when we show how and why a gene network is essential in embryonicdevelopment, can we say we understand its function.
5. Conclusion and prospects We have argued how cell-centered simulations, in particular the CPM, can elucidate mechanisms of biological development.We have argued that we can,and indeed must, separate the question of how genetics drives cell behavior fromthe question of how cell behavior drives morphogenesis.We have previouslyproposed a similar approach in modeling colonial stony-coral morphogenesis,where we assumed individual coral polyps were the central module of morpho-genesis Some authors argue that the energy-minimization approach of the CPM precludes consideration of the forces involved in cell–cell adhesion and cell motion .In theCPM cells move according to effective-energy gradients, rE: Thus, given an effective energy we can calculate the resulting cell motion and the force required tocreate such motion.In the highly viscous environment of the ECM, force isproportional to velocity, not acceleration, i.e., v; a relation we call the overdamped force– velocity response.Thus we can derive effective forces using therelation rE: Ongoing work aims to assign physical units to the effective energies.Ultimately we hope to derive CPM parameters, such as those involved incell adhesion and chemotaxis, from experimentally measured energies involved in theformation and breakage of bonds between cell adhesion molecules, and the effectiveforces individual filopodia and lamellipodia exert.
Currently, the CPM models the transport of signaling molecules in the ECM with a simple diffusion equation, ignoring advection due to cell and ECM movement.Intwo dimensions, nutrients or signaling molecules may move through a culture gelover which the cells move (see e.g., Ref. ).In three-dimensional simulations wecannot side-step advection.We are now developing a CPM-based advection–diffu-sion method to fix this unphysical anomaly (D.Dan, K.Chen and J.A.Glazier, to bepublished).These methods partition the ECM into tiny CPM cells; each of these fluidcells contains an attribute describing the current concentration of the advecting anddiffusing chemical.A volume constraint ensures that moving biological cells canpush the fluid cells.A superimposed diffusion equation describes flux betweenneighboring fluid cells.
The CPM is just one of a wide range of cell-centered modeling frameworks.Why do we prefer it to these alternative methods? Many cell-centered models describe R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 individual cells as points or spheres, ignoring that the shape of individual cells can bean essential determining factor in development.In the CPM, a cell's contact energywith surrounding cells and the ECM determines the cell's shape, while the surfacearea over which two cells adhere determines the forces needed to separate them.
Additional constraints can determine specific cell shapes, which may affect tissue-level patterning Another advantage of the CPM is its clear distinction between cell adhesion and cell attraction. Many cell-centered methods (e.g., Refs. approximate celladhesion as cell attraction, describing adhesive forces using potentials surroundingthe cells (a center-model formalism).However, molecular interactions over verysmall distances, at least an order of magnitude below the cell scale, cause adhesion.
Thus, in a physically correct model of cell adhesion, the cells must touch in order toadhere.The CPM better distinguishes between long-range and short-range attractiveand repulsive interactions.
As models and experimental data become more sophisticated, the cell-centered approximation will require extensions to both larger and smaller length-scales.
Integrating more microscopic models like BioSpice or Virtual Cell into the CPM ispossible in two fashions.They can precalculate or directly control CPM parametersor they can function as components in true hybrid models.Similarly, the CPM cancalculate complex materials properties for finite-element continuum models or caninterface directly with the finite-element mesh to produce a hybrid model.The keyadvantage of the CPM is that we need introduce only the minimal additionalalgorithmic complexity and computation time needed to correspond with the qualityof our existing experimental data (hence the suggestive funnel shape we employedin Ultimately, we hope that the cell-centered modeling approach will serve developmental biology as a hypothesis-generating and explanatory tool.It willassist developmental biologists to unravel how cell behavior drives tissue-leveland organ-level phenomena.Which cell behaviors are essential for observedtissue-level phenomena? Which gene networks are responsible for these essentialcell-behaviors? How do gain-of-function and loss-of-function mutations alterindividual cell behaviors, and how do these modifications lead to organism-levelknock-out phenotypes? Currently, many biologists seem to assume directcausal links between gene action and organism-level phenotypes, and considerthat these correlations represent a well-defined gene function.To truly under-stand gene-function, we must put the most essential module of development in thecenter: the cell.
We acknowledge the support from grants NSF-IBN-008365, NASA-NAG2-1619, from Indiana University's Pervasive Technologies Laboratories, BiocomplexityInstitute, College of Arts and Sciences and Office of the Vice President for Researchand from an IBM Innovation Institute award.We would also like to acknowledge R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 helpful discussions with Paulien Hogeweg, Wei Zeng, Gilberto Thomas, Stan Mare´e,Mark Alber, Cornelis Weijer, Stuart Newman, Philip Maini, Santiago Schnell andMark Chaplain.
[1] E.F. Keller, Making Sense of Life, Harvard University Press, Cambrige, MA, 2002.
[2] H.Kitano, Systems biology: a brief overview, Science 295 (2002) 1662–1664.
[3] L.Wolpert, Principles of Development, Oxford University Press, Oxford, 1998.
[4] A.M. Turing, The chemical basis of morphogenesis, Philos. Trans. Roy. Soc. B 237 (1952) [5] J.M.W. Slack, From Egg to Embryo: Determinative Events in Early Development, Cambridge University Press, Cambridge, 1983.
[6] I.Salazar-Ciudad, J.Jernvall, S.A.Newman, Mechanisms of pattern formation in development and evolution, Development 130 (2003) 2027–2037.
[7] T. Krul, J. Kaandorp, J.G. Blom, Modelling developmental regulatory networks, in: P.M.A. Sloot, D. Abramson, A.V. Bogdanov, J.J. Dongarra, A.Y. Zomaya, Y.E. Gorbachev (Eds.), ComputationalScience—ICCS 2003, Lecture Notes in Computer Science, vol.2657, Melbourne, Australia andSt.Petersburg, Russia, 2003, pp.688–697.
[8] B.M. Slepchenko, J.C. Shaff, I. Macara, L.M. Loew, Quantitative cell biology with the virtual cell, Trends Cell Biol.13 (2003) 570–576.
[9] M.Tomita, K.Hashimoto, K.Takahashi, T.Shimizu, Y.Matsuzaki, F.Miyoshi, K.Saito, S.
Tanida, K.Yugi, J.Venter, C.Hutchison III, E-CELL: software environment for whole-cellsimulation, Bioinformatics 15 (1999) 72–84.
[10] H.Meinhardt, Pathways and building blocks, in: G.Schlosser, G.
P.Wagner (Eds.
‘‘Modularity in Development and Evolution'', Nature 430 (2004) 970.
[11] G.von Dassow, E.Meir, Exploring modularity with dynamical models of gene networks, in: G.
Schlosser, G.P. Wagner (Eds.), Modularity in Development and Evolution, The University ofChicago Press, Chicago, 2004, pp.244–287.
[12] J.B. Bassingthwaighte, Strategies for the Physiome project, Ann. Biomed. Eng. 28 (2000) [13] M.Lantin, An environment for the simulation of biological cells, Ph.
D.Thesis, Simon Fraser University, 1999.
[14] D.M.Holloway, M.Lantin, Maintaining apical dominance in the fern gametophyte, Ann.Bot.89 (2002) 409–417.
[15] E.Palsson, A three-dimensional model of cell movement in multicellular systems, Futur.Gener.
Comp.Syst.17 (2001) 835–852.
[16] M.A. Kiskowski, M.S. Alber, G.L. Thomas, J.A. Glazier, N.B. Bronstein, J. Pu, S.A. Newman, Interplay between activator–inhibitor coupling and cell–matrix adhesion in a cellular automatonmodel for chondrogenic patterning, Dev.Biol.271 (2004) 372–387.
[17] H.J. Bussemaker, A. Deutsch, E. Geigant, Mean-field analysis of a dynamical phase transition in a cellular automaton model for collective motion, Phys.Rev.Lett.78 (1997) 5018–5021.
[18] J.K. Parrish, L. Edelstein-Keshet, Complexity, pattern and evolutionary trade-offs in animal aggregation, Science 284 (1999) 99–101.
[19] U.Bo¨rner, A.Deutsch, H.Reichenbach, M.Ba¨r, Rippling patterns in aggregates of myxobacteria arise from cell–cell collisions, Phys.Rev.Lett.89 (2002) 078101.
[20] M.Meyer-Hermann, A.Deutsch, M.Or-Guil, Recycling probability and dynamical properties of germinal center reactions, J.Theor.Biol.210 (2001) 265–285.
[21] S.Dormann, A.Deutsch, Modeling of self-organized avascular tumor growth with a hybrid cellular automaton, In Silico Biol.2 (2002) 1–14.
[22] D.Drasdo, R.Kree, J.S.McCaskill, Monte carlo approach to tissue-cell populations, Phys.Rev.E 52 (1995) 6635–6657.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 [23] D.Drasdo, G.Forgacs, Modeling the interplay of generic and genetic mechanisms in cleavage blastulation and gastrulation, Dev.Dyn.219 (2000) 182–191.
[24] D.Drasdo, S.Hohme, Individual-based approaches to birth and death in vascular tumors, Math.
Comput.Model.37 (2003) 1163–1175.
[25] T.J. Newman, R. Grima, Many-body theory of chemotactic cell–cell interactions, Phys. Rev. E 70 (2004) 051916.
[26] E.F. Keller, L.A. Segel, Model for chemotaxis, J. Theor. Biol. 30 (1971) 225–234.
[27] S. Peirce, E.J. Van Gieson, T.C. Skalak, Multicellular simulation predicts microvascular patterning and in silico tissue assembly, FASEB J.18 (2004) 731–733.
[28] D. Longo, S.M. Peirce, T.C. Skalak, L. Davidson, M. Marsden, B. Dzamba, De Simone, Multicellular computer simulation of morphogenesis: blastocoel roof thinning and matrix assembly inXenopus laevis, Dev.Biol.271 (2004) 210–222.
[29] J.A. Glazier, F. Graner, Simulation of the differential adhesion driven rearrangement of biological cells, Phys.Rev.E 47 (1993) 2128–2154.
[30] F.Graner, J.A.Glazier, Simulation of biological cell sorting using a two-dimensional extended Potts model, Phys.Rev.Lett.69 (1992) 2013–2016.
[31] P.Hogeweg, Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation, J.Theor.Biol.203 (2000) 317–333.
[32] N.J. Savill, P. Hogeweg, Modelling morphogenesis: from single cells to crawling slugs, J. Theor. Biol.
184 (1997) 229–235.
[33] A.F.M. Mare´e, P.Hogeweg, Modelling Dictyostelium discoideum morphogenesis: the culmination, Bull.Math.Biol.64 (2002) 327–353.
[34] M. Zajac, G.L. Jones, J.A. Glazier, Model of convergent extension in animal morphogenesis, Phys.
Rev.Lett.85 (2000) 2022–2025.
[35] A.F.M. Mare´e, P.Hogeweg, How amoeboids self-organize into a fruiting body: multicellular coordination in Dictyostelium discoideum, Proc.Natl.Acad.Sci.98 (2001) 3879–3883.
[36] J.A.Izaguirre, R.Chaturvedi, C.Huang, T.Cickovski, J.Coffland, G.Thomas, G.Forgacs, M.
Alber, G. Hentschel, S.A. Newman, J.A. Glazier, COMPUCELL, a multi-model framework forsimulation of morphogenesis, Bioinformatics 20 (2004) 1129–1137.
[37] S.Turner, J.A.Sherratt, Intercellular adhesion and cancer invasion: a discrete simulation using the extended Potts model, J.Theor.Biol.216 (2002) 85–100.
[38] W. Zeng, G.L. Thomas, J.A. Glazier, Non-Turing stripes and spots: a novel mechanism for biological cell clustering, Physica A 341 (2004) 482–494.
[39] P.Hogeweg, Computing an organism: on the interface between informatic and dynamic processes, Biosystems 64 (2002) 97–109.
[40] S.A. Kauffman, Metabolic stability and epigenesis in randomly connected nets, J. Theor. Biol. 22 (1969) 437–467.
[41] N.J. Savill, J.A. Sherratt, Control of epidermal cell clusters by notch-mediated lateral inhibition, Dev.
Biol.258 (2003) 141–153.
[42] M. Zajac, G.L. Jones, J.A. Glazier, Simulating convergent extension by way of anisotropic differential adhesion, J.Theor.Biol.222 (2003) 247–259.
[43] R.M.H. Merks, S.A. Newman, J.A. Glazier, Cell-oriented modeling of in vitro capillary development, in: P.M.A. Sloot, B. Chopard, A.G. Hoekstra (Eds.), Cellular Automata. Sixth InternationalConference on Cellular Automata for Research and Industry, Lecture Notes in Computer Science,vol.3305, Spinger, Berlin, 2004, pp.425–434.
[44] C.Kes-mir, R.J. De Boer, A spatial model of germinal center reactions: cellular adhesion based sorting of B cells results in efficient affinity maturation, J.Theor.Biol.222 (2003) 9–22.
[45] S.Turner, J.
A.Sherratt, D.Cameron, Tamoxifen treatment failure in cancer and the nonlinear dynamics of TGF-b; J.Theor.Biol.229 (2004) 101–111.
[46] A.Gamba, D.Ambrosi, A.Coniglio, A.De Candia, S.Di Talia, E.Giraudo, G.Serini, L.Preziosi, F.
Bussolino, Percolation morphogenesis and Burgers dynamics in blood vessels formation, Phys.Rev.
Lett.90 (2003) 118101.
R.M.H. Merks, J.A. Glazier / Physica A 352 (2005) 113–130 [47] J.D. Murray, On the mechanochemical theory of biological pattern formation with application to vasculogenesis, C.R.Biol.326 (2003) 239–252.
[48] R.M.H. Merks, A.G. Hoekstra, J.A. Kaandorp, P.M.A. Sloot, Polyp oriented modelling of coral growth, J.Theor.Biol.228 (2004) 559–576.
[49] J.A. Kaandorp, P.M.A. Sloot, R.M.H. Merks, R.P.M. Bak, M.J.A. Vermeij, C. Maier, Morphogenesis of the branching reef coral Madracis mirabilis, Proc.Roy.Soc.Lond.B Biol., inpress.
[50] E.Palsson, H.G.Othmer, A model for individual and collective cell movement in Dictyostelium discoideum, Proc.Natl.Acad.Sci.USA 97 (2000) 10448–10453.

Source: http://ontologiasparaendemias.xpg.uol.com.br/artigos/A%20cell%20centred%20approach%20to%20developmental%20biology.pdf